Probabilidad independiente

Para explicar la probabilidad independiente el mejor ejemplo que podemos usar es un lanzamientos de monedas, una moneda tiene una probabilidad de caer cara del 0.5 (HEAD) y de caer cruz del 0.5 (TAIL) las probabilidades de los distintos eventos siempre tienen que sumar 1, el problema que queremos resolver es encontrar la probabilidad de que salgan dos caras seguidas si tiramos la misma moneda dos veces (podemos representar esta probabilidad como P(H ? H) o P(H, H)) podemos construir una tabla de verdad para resolver la pregunta, sabemos que al tirar la moneda dos veces seguidas esto crea varias combinaciones:

puede que la moneda caiga cara dos veces seguidas (H, H), puede que caiga primero cara y despues cruz (H, T), que caiga cruz y despues cara (T, H) o que caiga cruz las dos veces (T, T), como recordamos cada parte de la moneda tiene la probabilidad de caer del 0.5, para conseguir la probabilidad de que caiga dos veces tenemos que multiplicar estas dos probabilidades esto seria 0.5 * 0.5 que da como resultado 0.25, como ambos lados de la moneda tienen la misma probabilidad de caer todas las combinaciones también tendran la misma probabilidad:

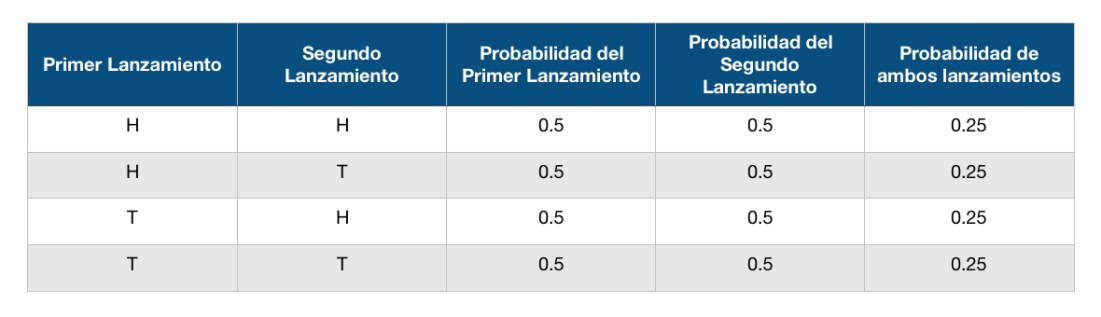
Es importante notar que si sumamos las probabilidades de todas las combinaciones el resultado es 1 (0.25 + 0.25 + 0.25 + 0.25 = 1)

Ahora imaginemos que tenemos una moneda cargada, esto quiere decir que un lado tiene más probabilidad de salir, por ejemplo la probabilidad de que salga cara es de P(H) = 0.7 y la probabilidad de que salga cruz es de P(T) = 0.3 y queremos encontrar la probabilidad de que salgan dos caras seguidas P(H, H), podemos construir la tabla de verdad y realizar las operaciones:

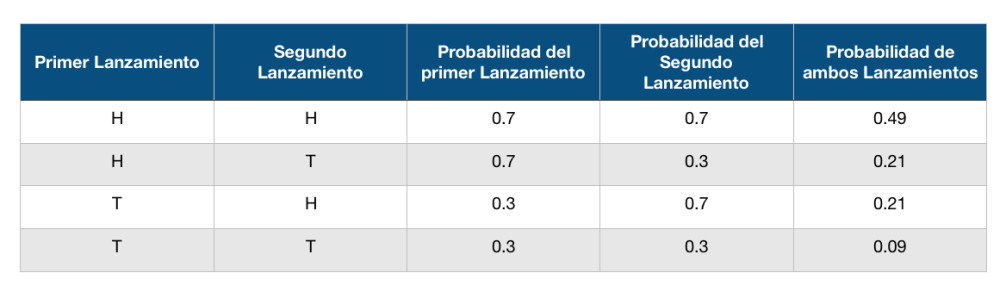
La probabilidad de P(H, H) con una moneda cargada es del 0.49, igualmente si sumamos las combinaciones suman a 1 (0.09 + 0.21 + 0.21 + 0.49 = 1)

También podemos usar una tabla de verdad si tenemos tres monedas, en este caso usaremos una moneda sin cargar con probabilidades P(H) = 0.5 y P(T) = 0.5 y queremos encontrar la probabilidad de que solo salga una cara en tres tiros:

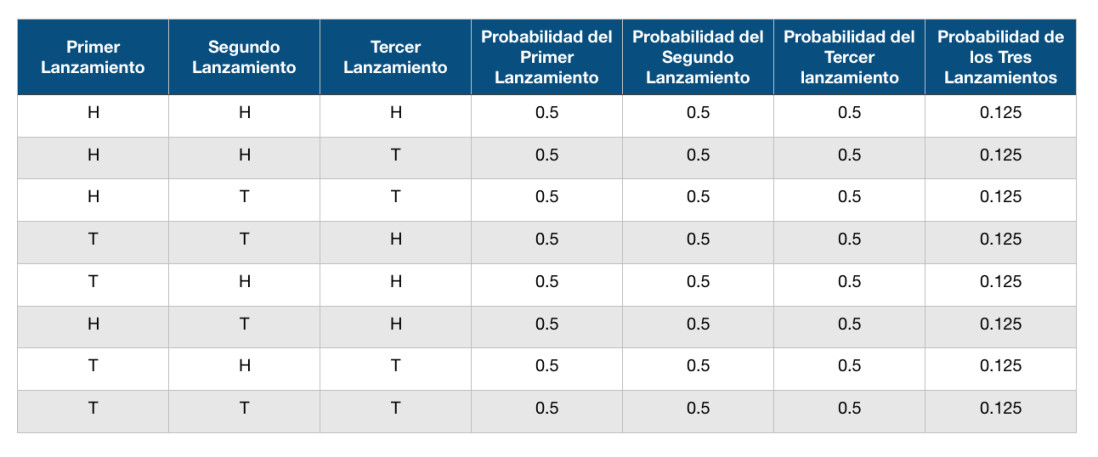
Sabemos que la probabilidad es la misma para las distintas combinaciones ya que la moneda no esta cargada, pero en este caso nosotros queremos las combinaciones donde solo salga una cara y podemos notar que existen tres combinaciones donde pasa esto:

en este caso hay que sumar estas tres probabilidades (0.125 + 0.125 + 0.125) para obtener la respuesta a la pregunta (0.375).

Ahora veamos un ejemplo con dados. Queremos saber la probabilidad de que lanzando dos veces un dado salgan dobles, sabemos que un dado tiene 6 lados y que cada lado tiene la misma probabilidad de salir (1/6), para obtener un doble el numero tiene que salir dos veces:

Ahora tenemos que sumar todas las combinaciones donde podemos obtener dobles que son 6 (0.02777777778 * 6) la respuesta es 0.1666666667.

Este tipo de probabilidad se llama independiente ya que la probabilidad del primer evento no afecta a la probabilidad del segundo evento y para encontrar las respuestas podemos multiplicar las probabilidades de los eventos.

Probabilidad condicional

Existe otro tipo de probabilidad donde la probabilidad de que pase un evento P(A) afecta a la probabilidad de que pase un evento P(B). Podemos representar la probabilidad condicional como P(Positive | Cancer) y es la probabilidad de que un estudio sea positivo dado que el paciente tiene cancer, en este caso la situación del paciente (si tiene cancer o no) afecta al resultado del estudio. Podemos tener dos respuestas del estudio:

P(Positive | Cancer) = 0.9

P(Negative | Cancer) = 0.1

esto indica que hay una alta probabilidad de que el estudio acierte y sea positivo si el paciente tiene cancer (90%) y que hay una probabilidad del 10% de que el estudio falle y salga negativo si el paciente tiene cancer, como podemos notar estas dos probabilidades suman 1, ahora también podemos tener las probabilidades de los estudios cuando el paciente no tiene cancer:

P(Positive | No Cancer) = 0.2

P(Negative | No Cancer) = 0.8

Para un paciente sin cancer el estudio puedar fallar y dar positivo el 20% de los casos y acertar y dar negativo un 80% de los casos. Estas dos probabilidades también suman 1.

En la probabilidad condicional tenemos que asumir que el evento B en la formula P(A | B) es verdad.

Con la probabilidad condicional también podemos crear una tabla de verdad, si queremos conocer la probabilidad de que un paciente tenga cancer y que el estudio sea positivo P(Positive ? Cancer) o P(Positive, Cancer) o de que un paciente no tenga cancer y que el estudio sea negativo P(Negative ? No Cancer) o P(Negative, No Cancer) podemos hacer lo siguiente:

Primero necesitamos las probabilidades de que un paciente tenga cancer o no tenga cancer:

P(Cancer) = 0.1

P(No Cancer) = 0.9

Ahora usando las probabilidades condicionales anteriores:

P(Positive | No Cancer) = 0.2

P(Negative | No Cancer) = 0.8

P(Positive | Cancer) = 0.9

P(Negative | Cancer) = 0.1

podemos crear una tabla de verdad:

Si queremos encontrar la respuesta a la primera pregunta P(Positive ? Cancer) tenemos que multiplicar la probabilidad de que el paciente tenga cancer P(CANCER) = 0.1 con la probabilidad de que el estudio dio positivo dado que el paciente tiene cancer P(Positive | Cancer) = 0.9 esto es 0.1 * 0.9 que da como resultado 0.09.

Si sumamos todas las probabilidades (0.09 + 0.01 + 0.18 + 0.72) el resultado es 1.

Podemos usar la probabilidad condicional con monedas, supongamos que tenemos dos monedas y una de ellas esta cargada

las probabilidades de la moneda sin cargar son:

P(H) = 0.5

P(T) = 0.5

las probabilidades de la moneda cargada son:

P(H) = 0.4

P(T) = 0.6

Ambas monedas estan en una bolsa donde donde no las podemos ver pero la moneda cargada es un poco mas grande que la otra moneda entonces es más facil que la saquemos.

la probabilidad de sacar la moneda grande es de:

P(C1) = 0.6

La probabilidad de sacar la moneda pequeña es de:

P(C2) = 0.4

si nos preguntan cual es la probabilidad de que sacando una moneda esta caiga cara dos veces seguidas P(H, H), podemos construir una tabla de verdad:

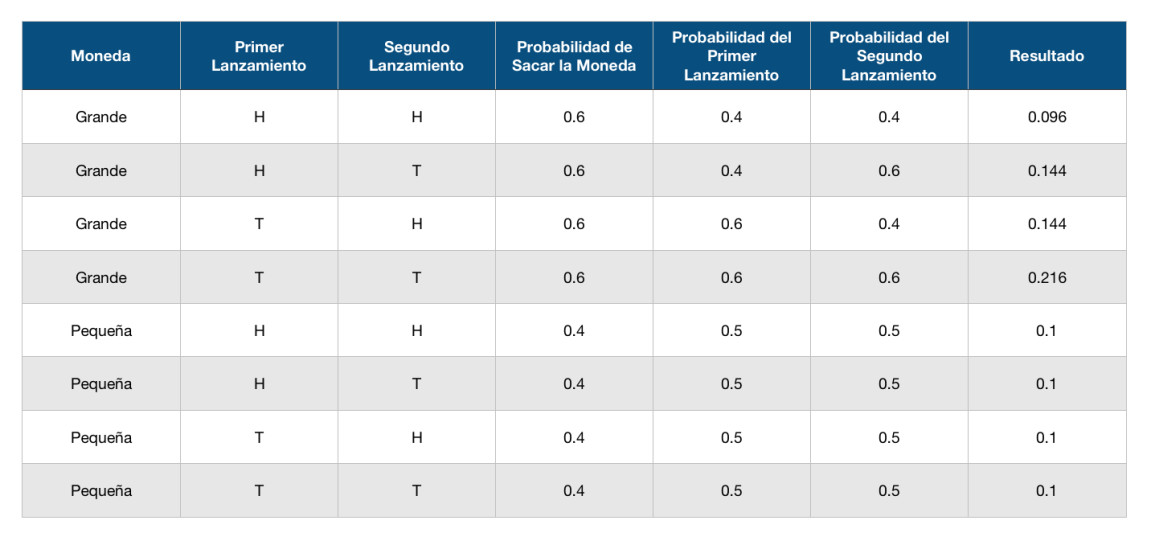
primero podemos comprobar que la suma de las probabilidades da uno

(0.1 + 0.1 + 0.1 + 0.1 + 0.216 + 0.144 + 0.144 + 0.096 = 1)

Ahora sabemos que cada moneda tiene diferentes probabilidades de salir y también diferentes probabilidades de que caiga cara o cruz, entonces tenemos que multiplicar la probabilidad de sacar cada moneda (0.6 o 0.4) por la probabilidad de que salga cara o cruz (0.4, 0.6) y (0.5, 0.5). Para responder la pregunta tenemos que sumar las combinaciones donde sale cara dos veces:

Si sumamos estas probabilidades tenemos el resultado de (0.096 + 0.1) = 0.196, 0.196 es la probabilidad de que sacando cualquier moneda y lanzandola dos veces caiga cara ambas veces.

A lo largo de esta sección hemos usado la siguiente formula:

Esto se lee: la probabilidad de que el evento A y el evento B ocurran al mismo tiempo es igual a la probabilidad del evento A multiplicada por la probabilidad de que suceda el evento B dado que el evento A ya sucedio, esta formula necesita que la probabilidad condicional ya este calculada como en el ejemplo de los estudios P(Positive | Cancer), aquí ya sabiamos la probabilidad de que el estudio sea positivo si la persona tiene cancer, si queremos calcular la probabilidad condicional usamos la formula:

La probabilidad de que suceda el evento A dado que ya sucedio el evento B es igual a la probabilidad de que sucedan los eventos A y B al mismo tiempo entre la probabilidad del evento B. Nosotros calculamos la parte P(A ? B) en los ejemplos anteriores ya que nos ayudara a comprender mejor la siguiente sección.

Teorema de bayes

El teorema de bayes es uno de los conceptos más importantes de la probabilidad y de la estadística, basicamente nos ayuda a responder la pregunta P(B | A) si se produjo un evento A cual es la probabilidad de que la causa haya sido el evento B.

Un ejemplo muy comun es el siguiente:

¿Cual es la probabilidad de que tengas cancer dado que el estudio dio positivo?.

P(Cancer | Positive)

Para contestar esta pregunta primero necesitamos las siguientes probabilidades:

Ahora necesitamos calcular la probabilidad conjunta que es lo mismo que: P(A, B) o P(A ? B)

Sumamos ambas probabilidades para obtener un normalizador: 0.09 + 0.45 = 0.54

y para obtener el resultado final tenemos que dividir las probabilidades conjuntas entre el normalizador:

para comprobar podemos sumar ambas probabilidades (0.8333333333 + 0.1666666667) el resultado es 1.

La respuesta a la pregunta es 0.1666666667 o un 16.66%.

Hay que tener cuidado de no confundir la probabilidad condicional y el teorema de bayes ya que la formula tiene una sintaxis similar, recordemos que en la probabilidad condicional obtenemos la probabilidad de un evento A que fue afectado por un evento B P(A | B) y en el teorema de bayes obtenemos la probabilidad de que un evento B haya causado un evento A P(B | A).

La formula para el teorema de bayes es la siguiente:

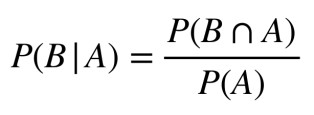
Si queremos resolver la misma pregunta:

¿Cual es la probabilidad de que tengas cancer dado que el estudio dio positivo?.

applicando la formula realizamos lo siguiente:

A es igual a la probabilidad de que el estudio salga positivo.

B es igual a que el paciente tenga cancer.

sabemos que P(B ? A) es igual a:

P(Cancer) * P(Positive | Cancer) == 0.1 * 0.9 = 0.09

para conseguir P(A) tenemos que sumar las probabilidades cuando el estudio es positivo:

entonces P(A) es igual a 0.09 + 0.45 y la formula queda de la siguiente manera:

P(B|A) = 0.09 / (0.09 + 0.45)

lo que da el mismo resultado: 0.1666666667

Distribución de probabilidad

Para obtener una distribución de probabilidad primero tenemos que calcular los valores de una variable aleatoria, por ejemplo el numero de veces que sale cara si lanzamos una moneda cinco veces, los posibles valores son:

0, 1, 2, 3, 4, 5

a cada uno de estos valores le asignamos una probabilidad y a esto se le llama distribución de probabilidad. Esta distribución se puede representar con una tabla, una grafica o con una función y la suma de todas las probabilidades tiene que ser 1.

Distribución binomial

La distribución binomial nos ayuda a encontar la probabilidad de un evento cuando existe una secuencia de eventos independientes y el evento solo tiene dos resultados (Falso, Verdadero | Cara, Cruz). Si ponemos el ejemplo de las monedas, ¿Cual es la probabilidad de que lanzando 5 veces una moneda caiga cara 3 veces?. Recordemos que hicimos una tabla de verdad para encontrar la respuesta, pero realizar esta tabla lleva tiempo, la función de probabilidad de una distribución binomial nos ayuda a resolver el problema más rapido:

Donde n es igual al numero de eventos, en este caso el numero de lanzamientos (n=5), k es igual al numero de eventos exitosos, que una moneda caiga cara 3 veces (k=3), p es igual a la probabilidad del evento exitoso, si hablamos de una moneda cargada donde P(H)=0.8 esta es la probabilidad del evento exitoso, con 1-p calculamos la probabilidad del evento contrario (que la moneda caiga cruz P(T)=0.2).

Recordemos que la sintaxis n! se refiere al numero factorial y este se calcula n * n-1 * n-2 * n-3 ... * 1 En el ejemplo seria 5 * 4 * 3 * 2 * 1.

Si sustituimos los valores en la formula queda de la siguiente forma:

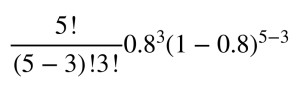
La respuesta es 0.2048, esta es la probabilidad de que salgan 3 caras en 5 tiros con una moneda cargada P(H)=0.8, P(T)=0.2.

Teorema del límite central

Para entender el Teorema del límite central o mejor conocido como Central limit theorem en Ingles primero recordemos que es una distribución normal.

Ejemplo de una distribución normal, también conocida como distribución de Gauss.

En la imagen anterior podemos ver como funciona una distribución normal, los valores de la media, la moda y la mediana tienen que ser iguales, la mayoria de los datos tienen que tener un valor similar. Esta imagen es un histograma, los histogramas grafican las veces que se repite un intervalo de datos, en la vida real sabemos que no todos los datos tienen una distribución normal, el teorema del límite central nos dice que si de una población sacamos n cantidad de datos, obtenemos la media de estos n datos, repetimos el proceso una cierta cantidad de veces y al final creamos un histograma con cada media que calculamos obtendremos una distribución normal. Pongamos un ejemplo con los lanzamientos de un dado, sabemos que cada lado del dado tiene la misma probabilidad de caer, si graficamos las veces que tiramos un dado obtendriamos un histograma como el siguiente:

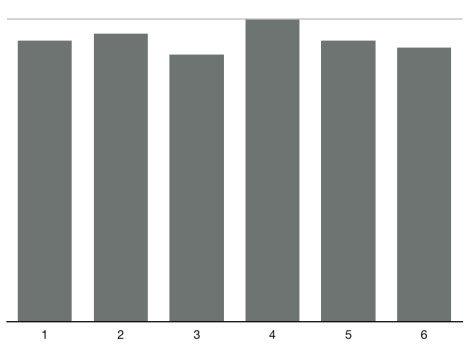
Podemos notar que no es una distribución normal, cada lado ha caido una cantidad similar de veces, si aplicamos el teorema a este problema y seleccionamos n lanzamientos del dado, calculamos la media de estos lanzamientos, repetimos el proceso muchas veces y al final todas las medias que calculamos las graficamos en un histograma obtendremos una distribución normal.

Un buen numero para n es 30, si seleccionamos 30 ejemplos de una población y aplicamos el teorema nos quedara una distribución normal más explicita, a veces podemos tomar menos ejemplos para llegar a una distribución explicita pero todo depende de la población que se analice.

Este teorema es muy importante en la estadística, con el podemos convertir cualquier distribución a una distribución normal y aprovechar las propiedades que este tipo de distribución tiene.

Intervalo de Confianza

Este intervalo tiene un rango de valores donde nosotros aseguramos que el verdadero valor esta ubicado.

Tenemos las alturas de 10 personas en centimetros:

168,167,165,170,175,180,181,178,182,178

Para calcular el intervalo de confianza necesitamos calcular la media y la desviación estandar:

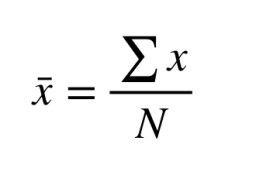
Media: 174.4

para obtener la desviación estandar primero calculamos la varianza:

Varianza: 36.24

Desviación estandar: 6.019966777317

La formula para calcular el Intervalo de Confianza es la siguiente:

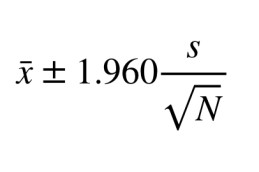
Intervalo de Confianza = 3.7312140652

Si agregamos el intervalo de confianza a la media 174.4 + 6.019966777317 y 174.4 - 6.019966777317 sabemos que la media real esta entre 168.3800332227 y 180.4199667773.

El valor que le sumamos y le restamos a la media se llama margen de error. En este caso el margen de error es de 3.7312140652.

No siempre podemos acceder o usar todos los datos de la población para realizar calculos, el intervalo de confianza nos permite saber en que rango se encuentra la media real usando solo una muestra de la población. Esta formula funciona mejor mientras la muestra tenga más datos ya que el rango del intervalo disminuye y con esto nos aproximamos más a la media real.

Como podemos notar la formula usa un numero especial 1.960, este numero indica un 95% de confianza, esto quiere decir que si tomamos una muestra el 95% de las veces la media real aparecera dentro del intervalo de confianza y el 5% de las veces la media real no aparecera dentro del intervalo. Por ejemplo supongamos que tenemos acceso a todos los datos (la población) y calculamos la media real que nos da 85, de todas las muestras que calculemos el 95% de esas muestras tendran un intervalo de confianza donde la media real parezca (85), puede ser un intervalo entre 83-86, 82-87, 84-87, etc. pero el 5% de esas muestras tendran un intervalo donde no aparezca la media real, como 80-83, 81-84, 86-88, etc. Lamentablemente no sabremos cual es la media real sin usar la población pero podemos estar seguros el 95% de las veces que la media real se encontrara en el intervalo que calculemos.

Hipótesis

La hipotesis es un metodo estadistico para tomar decisiones. En este metodo tenemos una hipótesis que creemos es verdad (H0 Hipótesis nula) y una hipótesis que contrasta a esta hipótesis (H1 Hipótesis alternativa). Veamos un ejemplo:

Supongamos que conseguimos una moneda que creemos es justa, esto quiere decir que tiene la misma probabilidad de que caiga cara P(H) = 0.5 y que caiga cruz P(T) = 0.5, nuestra Hipótesis nula indica que la moneda es justa H0 P(H) = 0.5 y la Hipótesis alternativa indica que la moneda no es justa H1 P(H) != 0.5, para comprobar si la Hipótesis nula es correcta necesitamos experimentar y lanzar la moneda unas cuantas veces.

Si lanzamos la moneda 10 veces necesitamos las probabilidades de que caiga cara de cero a diez veces. Podemos obtener estas probabilidades usando la función de probabilidad de la distribución binomial:

La probabilidad de que en diez lanzamientos una moneda justa caiga cara 0 veces, 1 vez, 2 veces, ...etc.

Podemos notar que la probabilidad más alta es cuanto la moneda cae cara 5 veces en 10 lanzamientos ya que nuestra hipótesis nula indica que la moneda es justa P(H) = 0.5, ahora realizamos el experimento y lanzamos la moneda diez veces obteniendo los siguientes resultados:

1, 0, 1, 1, 0, 0, 1, 1, 0, 1

El ultimo paso es encontrar la región crítica donde la hipótesis nula se descarta, esta región tiene que ser igual o menor al 5% de la probabilidad total (0.05) (One-tailed test). En este problema si nuestra moneda esta cargada la probabilidad de P(H) puede ser menor o mayor a 0.5 por esto tenemos que buscar en ambos extremos de la tabla las probabilidades que no sumen mas del 2.5% en cada lado, a esto le llamamos Two-tailed test.

Las primeras dos probabilidades de la izquierda suman 0.0107421875 esta es el región crítica del lado izquierdo, en este caso no podemos sumar la tercera probabilidad porque nos pasariamos del 2.5%, en la derecha obtenemos las mismas dos probabilidades que también suman 0.0107421875, esta es el región crítica del lado derecho, si sumamos los porcentajes de ambos lados obtenemos 0.021484375 que no pasa del 5% de la probabilidad total entonces podemos proseguir. Las secciones marcadas con rojo son las regiones críticas y la que esta en azul es el area segura. En nuestro experimento obtuvimos 6 caras, como podemos notar la columna donde esta el 6 es el area segura, podemos confirmar que la hipótesis nula es correcta, si hubiéramos obtenido un numero de caras menor a dos o mayor a 8 tendriamos que rechazar la hipótesis nula y aceptar la hipótesis alternativa.

Al igual que pasa con el intervalo de confianza en la hipotesis también tenemos un margen de error del 5%. Este margen de error es el mismo que usamos para encontrar la región crítica.

Error tipo 1

El error tipo 1 sucede cuando rechazamos la hipótesis nula cuando esta es correcta.

Error tipo 2

Este error sucede cuando la hipótesis nula es incorrecta y nosotros no la rechazamos.